先日のプロパラ会で齋藤夏雄さんの『詰将棋の世界』出版裏話を楽しく聞かせていただいた。その中に、一松信先生からの1枚の葉書が連載第8回と9回を書かせたという話があった。

なるほどそれで唐突に「詰将棋とコンピュータ」だったのか……。

一松先生の本は何冊も読ませていただいたが印象が強いのは『教室に電卓を！』だ。

興味深い教材の提案がいくつもあり面白かった。

それで続刊も購入したが、こちらは高校内容が主だったのでざっと流し読みをしただけで終わらせてしまった。

中学校でも一人１台のタブレットという時代に電卓なんてもう時代遅れかと思われるかもしれないが、今読んでもとても示唆に富んだ優れた内容だと思う。

しかし『教室に電卓を！III』1986年にもう「還暦を迎えて」と書いてあるんだけれど……いまだにお元気なんですね！

その一松先生から筆者も１枚の葉書をいただいたことがある。
前に書いたことあるけど読んだ人も忘れているくらい前だと思うので今回の「関係ない話」はこれでいこう。

中学校の１年生で正多面体というものを学ぶ。

正多面体とはプラトンの多面体のことで合同な正\(n\)角形がどの頂点にも\(m\)個集まった閉じた立体で凸なもののことをいう。

この正多面体\((n,m)\)は5つ存在し、5つしか存在しない。

正四面体\((3,3)\)

正六面体\((4,3)\)

正八面体\((3,4)\)

正十二面体\((5,3)\)

正二十面体\((3,5)\)

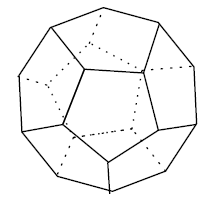
正十二面体の図が酷いが筆者の手書き(?)なのでお許しあれ。

当時、筆者は教員採用試験に落ちて、某進学塾で働いていた。
そこはけっこう頭の良い子どもが揃っていたので、少し難しい問題が必要だった。
そこで「正多面体の表面積と体積を中学範囲の数学で計算せよ」という課題を考えた。

試してみると正十二面体の表面積は二重根号になるので結果は高校範囲になるが、求めるだけなら中学範囲で問題ないことが分かった。

そのとき書いたのが次のテキストだ。

中学数学で求める正多面体の体積(1)(2)

(pdfにしたのはずっと後）

そのとき、自分の計算があっているのか答合わせをしたくなった。
今だったらインターネットで検索すれば数秒で正解に辿りつける。
しかし当時はそんなものはなかった。

そこで探しだして入手したのが一松先生の本だった。

こちらはまだ入手可能なようだ。Amazonへのリンクもつけておこう。

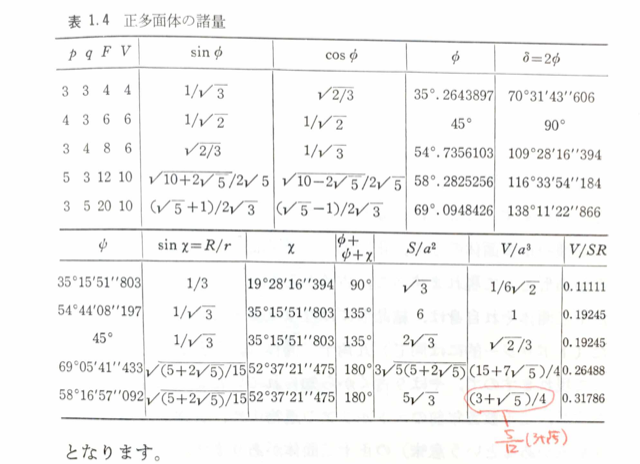
で、さっそく表を見つけて自分の出した値と比べてみると……1箇所だけ違う。

正二十面体の体積、本に書いてある値は\(\displaystyle\frac{3+\sqrt{5}}{4}\)だが、筆者の計算では\(\displaystyle\frac{5(3+\sqrt{5})}{12}\)だった。

今だったら、自分が計算間違いしたのだろうと思うだろう。
しかし、当時はまだ元気だったので、次のように推理した。

\(\displaystyle
\begin{eqnarray*}
\frac{3+\sqrt{5}}{4}:\frac{5(3+\sqrt{5})}{12}
&=&\frac{1}{4}:\frac{5}{12}\\
&=&3:5\\
&=&12:20
\end{eqnarray*}
\)

つまり一松先生は表を作成するのに学生に計算をさせ、その学生は正\(n\)角錐の体積を20倍するべき所を12倍してしまったのではないか。

他にも次のような誤植も見つけたので、「誤植を見つけました」と一松先生に手紙を書いたのだ。

それで一松先生から返事の葉書を頂いたという次第だ。

さて、前回いくつか問題を出して好評だった(?)ので、今回も中学1年生向けの正多面体がらみの問題をいくつか紹介しよう。

第1問

中学生には正多面体を次のように定義する。

では2の条件はなぜ必要か？また、へこみのないという条件はなぜ必要か？

第2問

1辺の長さが等しい5つの正多面体を体積の小さい順に並べなさい。
また、この中で体積がちょうど整数倍になっているのはどれとどれ？

第3問

1辺の長さが等しい正四面体と正八面体を、それぞれ1つの面をノリでピッタリ貼り合わせた。何面体ができるか

第4問

正六面体の展開図は11種類あるが、双対な正八面体の展開図も11種類ある。全部見つけなさい。

第5問

サッカーボール(色々あるけど正五角形と正六角形でできた最も有名なヤツ)はどの多面体を削って作ることが可能か。

第6問

名刺を3枚組合わせて作った次の図形はどの正多面体の骨組みか。

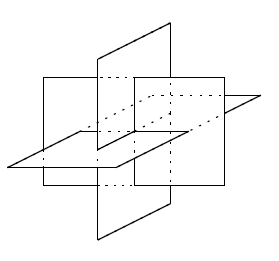
第7問

正十二面体から8個の頂点をうまく選んで正六面体を作れ。

第8問

正四面体を1つの平面で切断して、切断面が正方形になるようにせよ。

解答篇

第1問

2の条件が必要なのは写真のようなデルタ多面体をオミットするため。

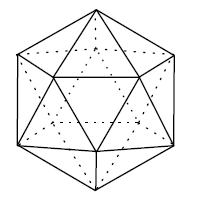
へこみのないという条件は正二十面体のため。

実際に骨組みで模型を作ってみると正十二面体などグラグラなのにへこまない。
正二十面体はガッチリしているのに、これだけへこんじゃうんだよね。
筆者にとっては凄く意外。

第2問

1辺の長さが等しい5つの正多面体を体積の小さい順に並べなさい。

\(正四面体＜正八面体＜正六面体＜正二十面体＜正十二面体\)

これは名前に惑わされるなよというだけの問題。

\(正四頂体＜正六頂体＜正八頂体＜正十二頂体＜正二十頂体\)

と書けば当たり前すぎる問題。
「球に内接させたとき最も体積が大きくなるのは」という問題でも良い。

体積がちょうど4倍になっているのは正四面体と正八面体。
理由は次問で。

第3問

七面体。
正四面体と正八面体の2面角は補角になっている。

これは1辺2の正四面体を考え、それぞれの頂点から4つの1辺1の正四面体を削り取ってみると分かる。
残るのは1辺1の正八面体だ。

体積は\(2^3=8\)から\(8-4=4\)なので4倍になる。

第4問

ネットで直ぐ検索できるから略。
双対な立体って不思議だ。
11種類の展開図にも対応関係があるはずだが、どれとどれが対応しているのか考えてみられては？

第5問

正二十面体。
C60フラーレンで有名なので解説は不要だろう。

ところで半正多面体って慣れません。

第6問

証明するのは中学3年生で三平方の定理を学んでから。

第7問

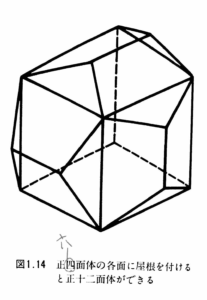
誤植の図にあるので略。

第8問

これ昔、王様のなんちゃらという店でパズルとして売っていた。
人間って左右対称にできているから、こんな簡単なものでもパズルになってしまうから面白い。

さて、最後に一松先生からの葉書には何と書かれていたか。
筆者の推理は完璧に当っていたようだ。
そして、もうちょっと早く教えてくれていたら増刷に間に合ったのに！ということだった。

皆さん、やはり初版は買ってはいけないということなのですね。
最近は増刷されない本が多いので、直ぐに買いますが。

そして『詰将棋の世界』増刷おめでとうございます。
祝、増刷出来！

Tweet