たまってきた宿題を片付ける二人であった。

金さんの方法が\((x+a)(x+b)\)の形に因数分解できる問題だったら、必ず有効であることを証明しなさい。

　
金さん　僕の方法ってどんなんだっけ。

銀さん　このやりかたじゃなかった？公式1ではなく、公式2と4を使う方法。

\(\begin{eqnarray}
&&x^2+120x+3599\\
&=&x^2+120x+3600-3600+3599\\
&=&x^2+120x+3600-1\\
&=&(x+60)^2-1^2\\
&=&(x+60-1)(x+60+1)\\
&=&(x+59)(x+61)
\end{eqnarray}\)

金さん　あそうか。それならできそうだ。

\(\begin{eqnarray}
&&(x+a)(x+b)\\
&=&x^2+(a+b)x+ab \\
&=& x^2+(a+b)x+\left(\frac{a+b}{2}\right)^2+ab-\left(\frac{a+b}{2}\right)^2\\
&=& x^2+(a+b)x+\left(\frac{a+b}{2}\right)^2+\left(\frac{4ab-a^2-2ab-b^2}{4}\right)\\
&=& x^2+(a+b)x+\left(\frac{a+b}{2}\right)^2-\left(\frac{a^2-2ab+b^2}{4}\right)\\
&=& \left(x+\frac{a+b}{2}\right)^2-\left(\frac{a-b}{2}\right)^2\\
\end{eqnarray}\)

これで、いいよね。

銀さん　うん。因数分解できる場合は2乗の差の形になることが示されているから、これで良さそうね。

銀さんの方法でなぜ
「たして\(11\)」「かけて\(12\times(-15)=-180\)」
の2数を見つければ良いのかを証明しなさい。

金さん　これは\(12x^2+11x-15\)を因数分解する方法だったね。

銀さん　やってみるわ。
\(\begin{eqnarray}
&&(ax+b)(cx+d)\\
&=&acx^2+(ad+bc)x+bd\\
\end{eqnarray}\)

これで充分ね。
かけて\(abcd\)、たして\((ad+bc)\)である2数というのは\(ad\)と\(bc\)。
わかってみると当たり前すぎる話だったわ。

\(x\)軸を幅\(h\)で均等に分割する。それぞれの\(x\)座標に対応する\(y=ax^2\)上の点を、最初の2点は任意に選び結ぶ。
以降は順にその1つ外側同士、または内側同士を順に結んでいく。
これらの線分がすべて平行になることを証明せよ。

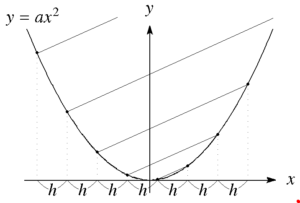
金さん　これは簡単。問題文がややこしそうになっているだけだ。

2乗比例のグラフと交わる直線

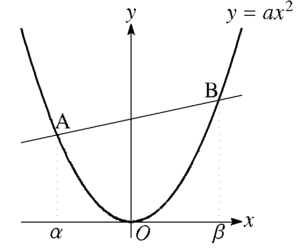
\(\mbox{AB}の傾き=a(\alpha+\beta)\)
\(\mbox{AB}の切片=-a\alpha\beta\)
したがって
\(\mbox{AB} : y=a(\alpha+\beta)x-a\alpha\beta\)

この定理を証明したのだから\(\alpha\)が\((\alpha-h)\)、\(\beta\)が\((\beta+h)\)になっても、その和は\((\alpha+\beta)\)で一定だ。したがってどれも平行。ここで\(h\)は正と負どちらでもOK。

銀さん　さすがね。交点の\(x\)座標を同じだけ離したり近付けたりしてもすべて平行になるということね。

すべての抛物線(\(y=ax^2\))は相似であることを証明せよ。

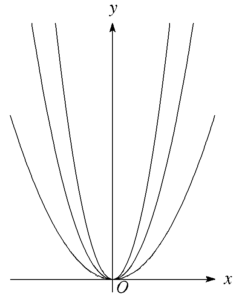
金さん　これはなんとなくわかるんだけれど、何をいえば証明になるかが判らない。
銀さん　玉さんの授業でかならず\(y=x^2\)の拡大グラフと\(y=\displaystyle\frac{1}{10}x^2\)のグラフを描かされるじゃない。あれがヒントかもよ。

金さん　そういえば描いたっけな。

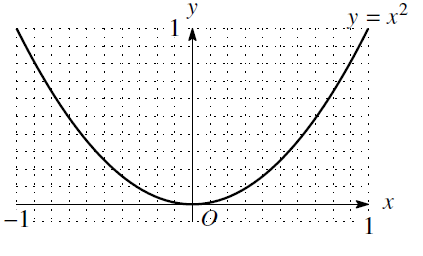
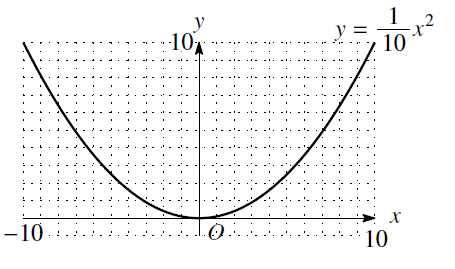
ん？とすると目盛りが10倍で一致するということは、相似比は\(1：10\)……とそんなに単純でいいの！？
それじゃ逆に\(y=2x^2\)のグラフは\(y=x^2\)のグラフの\(\displaystyle\frac12\)の縮小になっているというの？

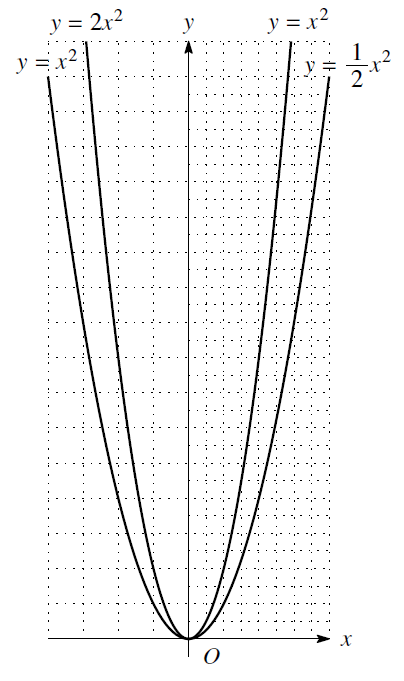
うわっ本当だ。右側だけ目盛りを細かくしたら、左側で\(y=x^2\)のグラフは右側では\(y=\displaystyle\frac12x^2\)のグラフに、左側で\(y=2x^2\)のグラフは右側では\(y=x^2\)のグラフになっちゃった。

そうか、\(y=\displaystyle\frac{1}{n}x^2\)のグラフが\((n,n)\)を通るということは気づいていたんだけど。

なんだ、このことを知っていたらどれも目盛りの数字を書き換えるだけで良かったのか。

銀さん　\(y=x^2\)のグラフと\(y=ax^2\)のグラフの相似比が\(1:\displaystyle\frac{1}{a}=a:1\)ということは、\(y=ax^2\)と\(y=bx^2\)のグラフの相似比は\(b:a\)になりそうね。

金さん　でも証明はなにをいえばいいのかな。

銀さん　相似の位置にあるということをいえばいいのではないかしら。

金さん　そうか、相似の中心は原点\(O\)だから対応する点が一直線に並んでいればいいんだ。

銀さん　そこでこないだの定理が使えるというわけね。､

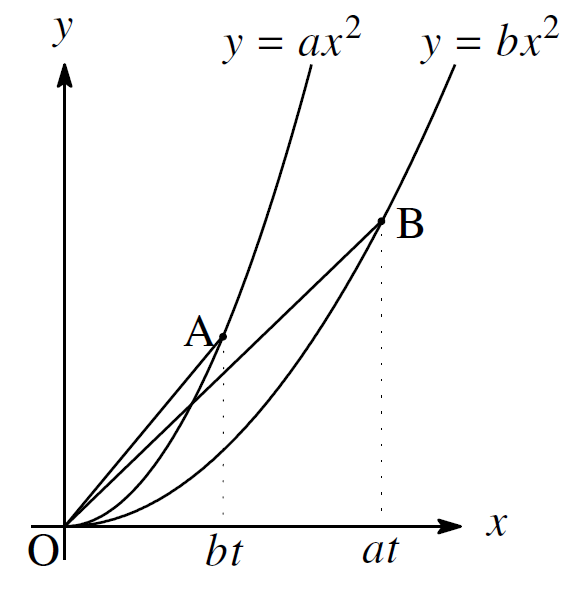
\(y=ax^2\)上の点をA(\(x\)座標は\(bt\))、\(y=bx^2\)上の点をB(\(x\)座標は\(at\))とすると、OAの傾きは\(abt\)、OBの傾きも\(abt\)だからO、A、Bは一直線上に並ぶ。つまり\(OA:OB=bt:at=b:a\)。

金さん　すなわち\(y=ax^2\)と\(y=bx^2\)は相似で、相似比は\(b:a\)というわけだ。

銀さん　最後だけいうなんてズルくない？

Tweet