たまには数学の問題を考えて、頭をリラックスさせましょう。
もちろん私が出題するのですから、数学といっても義務教育レベルの問題です。
今日は美代子であることを証明してもらいます。
ここでいう美代子とは
のことではありません。
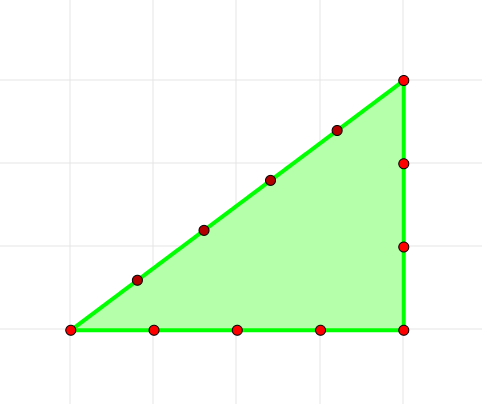
最小のピタゴラス三角形。3辺の長さの比が\(3:4:5\)である直角三角形のことです。
第1問
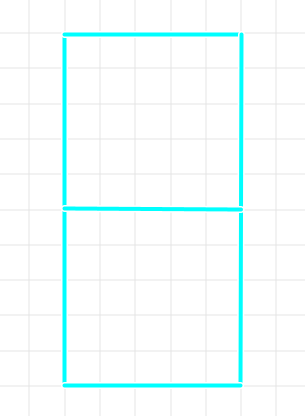
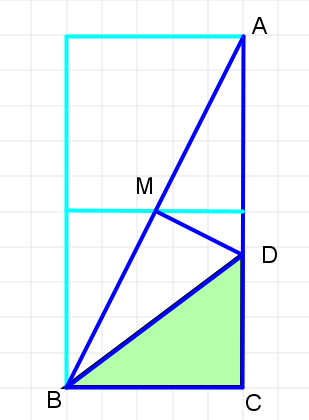
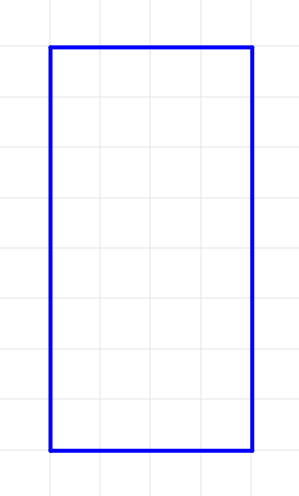
正方形を二つ縦に並べる。
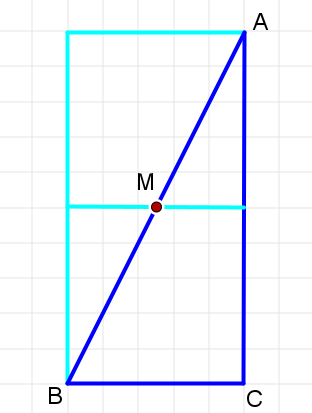
直角三角形ABCを描く。
斜辺ABの中点Mをとる。
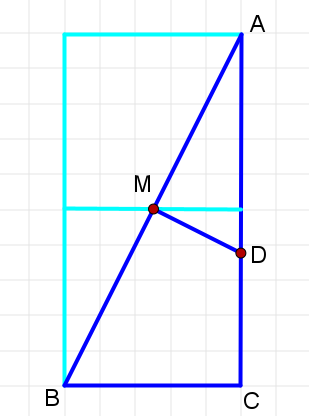
Mから垂線をひき、ACとの交点をDとする。
BDを結ぶ。
△DCBが美代子であることを示せ
問2
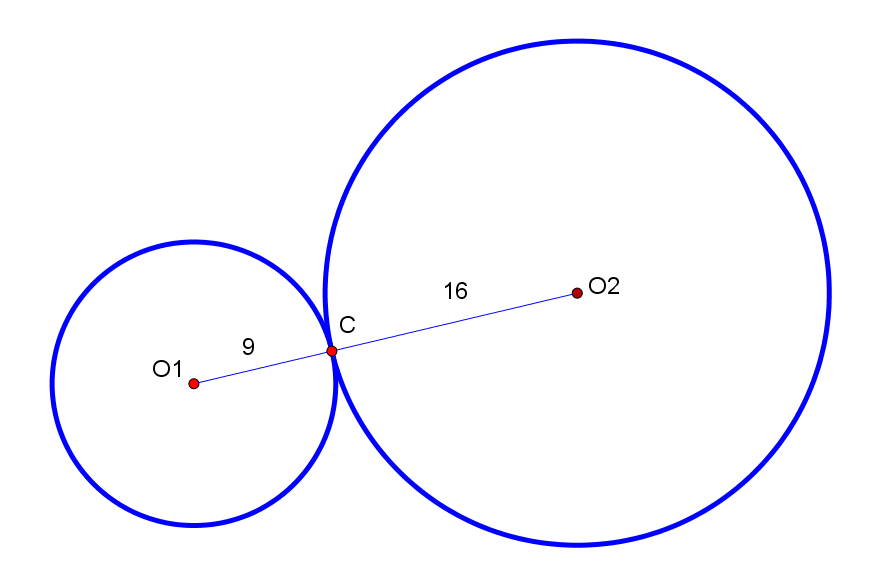
半径9の円と半径16の円を外接させて描き、接点をCとする。
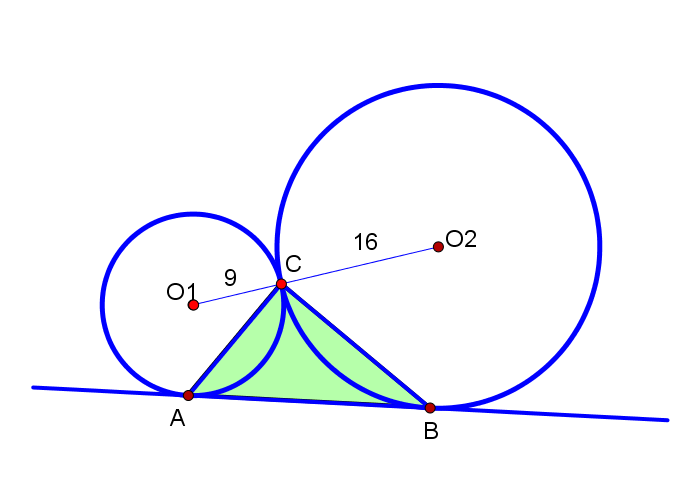
2つの円の共通外接線を引き、接点をそれぞれA、Bとする。
AC、BCを結ぶ。
△ABCが美代子であることを示せ
問3
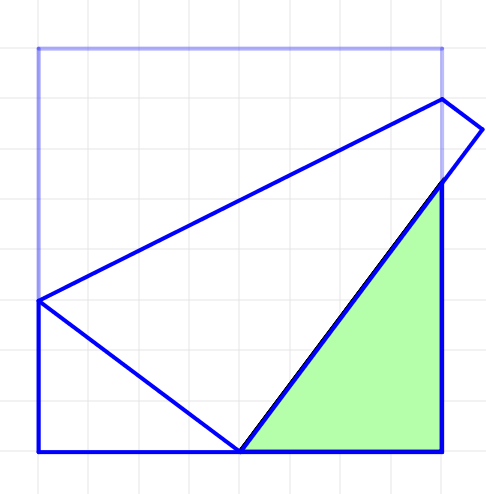
正方形の折り紙を用意する。
左上の頂点が下辺の中点に重なるようにおる。
色のついた三角形が
美代子であることを示せ
問4
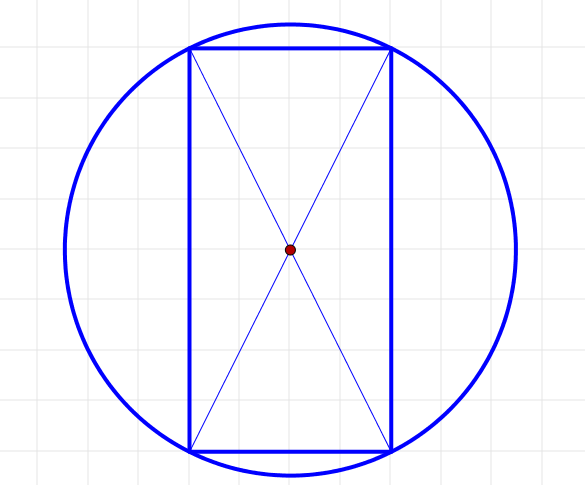
縦横の比が\(2:1\)の長方形を描く。
長方形の外接円を描く。
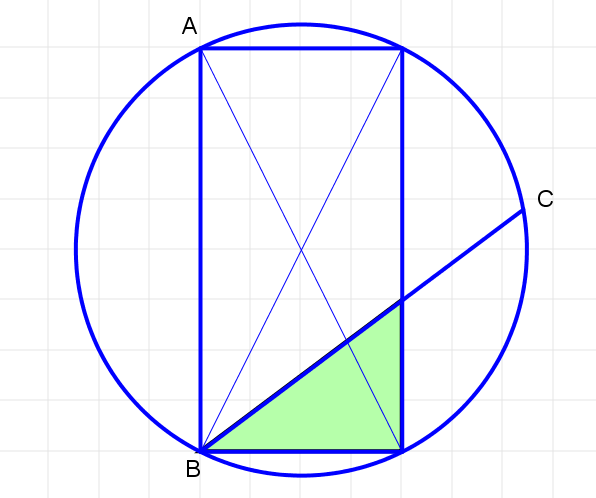
円周上に\(BA=BC\)となる点をとり、BCを結ぶ。
色のついた三角形が
美代子であることを示せ
解答
要望があれば書きますが、不要でしょう。
今年の都立入試問題を見ていて問4を思いつきました。
問1は問4をシンプルにしたものです。
問2は \(9:16=3^2:4^2\) ですから、いかにも作った問題なのが弱点ですね。
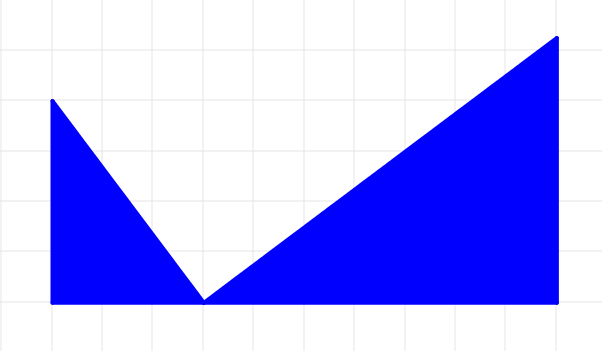
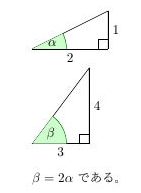
問2と問3は見かけは異なりますが、相似な三角形を下のように並べた形とみれば、実は同じ問題です。
そして問3には中点を使っているので実は問1と同じ、私が傾き2の直角三角形と呼んでいる問1の \(1:2:\sqrt{5}\) の三角形が元になっています。
とすると4問とも実は同じ問題に過ぎないということになりますが、そもそも美代子は傾き2の直角三角形と密接な関係にあるということなのかも知れません。
さらにこの元ネタをばらすと、某掲示板に浦壁さんが貼ってくれた次の問題に帰着します。
Tweet