このテキストは関係ない話(43)抛物線の性質のつづきです。
2乗比例のグラフの接線
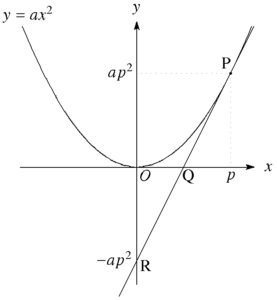
\(\mbox{PR}の傾き=2ap\)
\(\mbox{PR}の切片=-ap^2\)
したがって
\(\mbox{PR} : y=2apx-ap^2\)
この定理を承認して、抛物線の性質について調べます。
課題
パラボラアンテナは回転抛物面でつくられる。なぜ抛物線が利用されるのか、その理由を確認しなさい。
銀さん パラボラアンテナって衛星放送を受信するためのアンテナだったわよね。
金さん そういうのはおいらが詳しいよ。
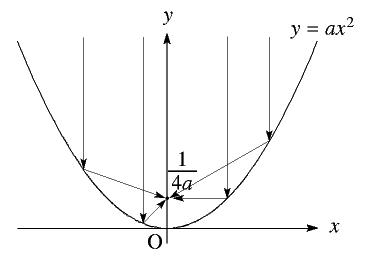
パラボラアンテナは平行線を集める性質を持っているんだ。
放射状に電波を飛ばすと進むにつれてどんどん弱くなっていくのはわかるだろう。
平行に電波を飛ばせば平行線の間隔は変わらないから遠くまで電波を飛ばすことができるんだ。
最近流行っているキャンプ用具でも「ソーラー調理器」とか「サニー調理器」という名前で売っているよ。


銀さん つまり放物線は平行線を反射して同じ点に集める性質を持っているということね。
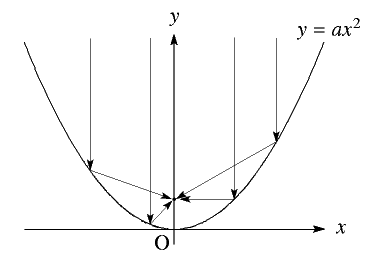
金さん そういうこと。それを証明すればいいんだと思う。
でも、直線にぶつかれば入射角と反射角が等しいようにはね返すんだろうことはわかるけれど、放物線は曲線だよね。
銀さん 当たる点は1点だから、その点における接線で考えれば良いのではないかしら。
金さん そうかそれでこないだの
\(y=2apx-ap^2\)
という接線の公式が役立ってくるわけだね。
それにしても難しそうだな。
銀さん いつもの通り、まずは易しい問題で練習しましょう。
金さん それじゃぁ、\(y=\displaystyle\frac14x^2\)と\(x=8\)がぶつかった場合で考えてみようかな。
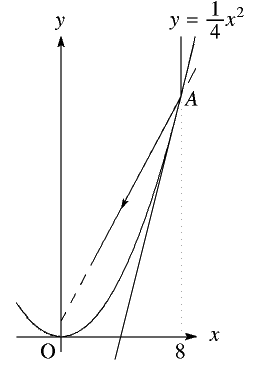
この場合接線は \(y=4x-16\)、\(x=8\) とは点\((8,16)\)でぶつかって、\(\ldots\) どこにいくんだろう?
\(A(8,16),B(8,20),C(9,20)\) という\(\triangle ABC\)を考える。
これと合同な\(\triangle AB’C’\)を考えてみようか。
もちろん\(CAC’\)は直線だよ。
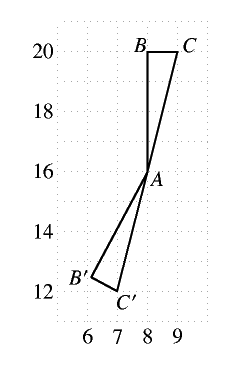
\(C'(7,12)\)はわかっているから\(B’\)の座標を計算してみる。
\(B'(a,b)\)とおいて、
\(B’C’=1\) だから \((a-7)^2+(b-12)^2=1^2\)
\(AB’=4\) だから \((a-8)^2+(b-16)^2=4^2\)
展開して加減法を使うと \(2a+8b=112\)
整理すると \(a+4b=56\)
う~ん、やるしかないのかな?
\(a=56-4b\) を \((a-7)^2+(b-12)^2=1^2\) に代入する。
\((4b-49)^2+(b-12)^2=1\)
展開して整理すると
\(17b^2-416b+2544=0\)
解の公式を用いて
\(\begin{eqnarray*}
b&=&\displaystyle\frac{416\pm\sqrt{416^2-4\times17\times2544}}{2\times17}\\
&=&\displaystyle\frac{416\pm\sqrt{173056-172992}}{34}\\
&=&\displaystyle\frac{416\pm\sqrt{64}}{34}\\&=&\displaystyle\frac{416\pm8}{34}\\
&=&\displaystyle\frac{208\pm4}{17}\\
&=&\displaystyle\frac{212}{17} or \displaystyle\frac{204}{17}
\end{eqnarray*}\)
ふぅ。解の公式は偉大だ。
このとき\(a\)の値を求めると、
\(a=56-\displaystyle\frac{4\times212}{17} or 56-\displaystyle\frac{4\times204}{17}\)
\(a=\displaystyle\frac{104}{17} or \displaystyle\frac{136}{17}\)
ここで \(a<7\) なので \(a=\displaystyle\frac{136}{17}\) は問題に適さない。
したがって \(a=\displaystyle\frac{104}{17}, b=\displaystyle\frac{212}{17}\)
\(B’\left(\displaystyle\frac{104}{17},\displaystyle\frac{212}{17}\right)\) とわかったので\(AB’\)の傾きが求められる。
\(\begin{eqnarray*}
AB’の傾き&=&\frac{16-\displaystyle\frac{212}{17}}{8-\displaystyle\frac{104}{17}}\\
&=&\displaystyle\frac{272-212}{136-104}\\
&=&\displaystyle\frac{60}{32}\\
&=&\displaystyle\frac{15}{8}
\end{eqnarray*}\)
やっと落ち着いた数になってくれたぞ。
えーと、\(AB’\)は傾き \(\displaystyle\frac{15}{8}\) で点\((8,16)\) を通る直線だから
\(y=\displaystyle\frac{15}{8}(x-8)+16\)
\(y=\displaystyle\frac{15}{8}x+1\)
ということは \((0,1)\) らしいね!
いやいや大変な計算だった。
銀さん 2次方程式でない別の式を立ててみたら?
\(\triangle ABC\)と\(\triangle AB’C’\) は線対称なのだから
対称軸を求めてみると \(A(8,16)\) を通って\(CC’\)に垂直な直線。
つまり \(y=-\displaystyle\frac14x+18\) ね。
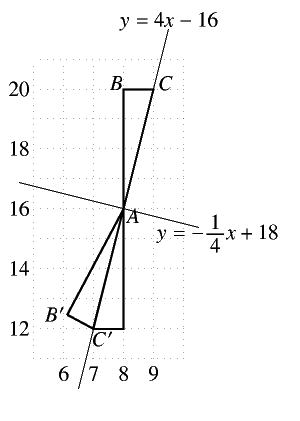
\(BB’\)の中点がこの直線上にあるわけだから
中点\(\left(\displaystyle\frac{a+8}{2},\displaystyle\frac{b+20}{2}\right)\) を代入して
\(\displaystyle\frac{b+20}{2}=-\displaystyle\frac{a+8}{8}+18\)
整理すると
\(a+4b=56\)
同様に\(B’\)は \((8,12)\) とも \(y=4x-16\) で対称なのだから
中点\(\left(\displaystyle\frac{a+8}{2},\displaystyle\frac{b+12}{2}\right)\) はこの直線上にある。
\(\displaystyle\frac{b+12}{2}=\displaystyle\frac{4(a+8)}{2}-16\)
整理すると \(4a-b=12\)
この連立方程式を解いて
\(\cases{a=\displaystyle\frac{104}{17}\\ b=\displaystyle\frac{212}{17}}\)
金さん なるほど連立2元1次方程式でも求められるんだ。
それでも結構な計算量があるよね。
銀さん 最初にもっと易しい練習問題を用意するべきよ。
私だったら接線の傾きが1になる場所を探すわ。
\(y=\displaystyle\frac14x^2\) なら
\(\displaystyle\frac{2p}{4}=1\) を解いて \(p=2\)
\((2,1)\) ね。
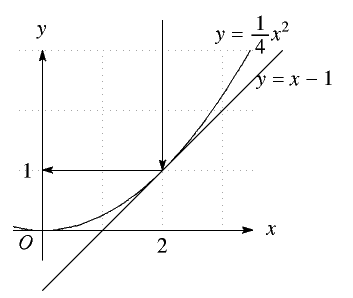
接線は \(y=x-1\) だから \((2,1)\) でぶつかったら水平線になるはず。
やはり \((0,1)\) を通るわね。
金さん ちぇっ、あまり易しすぎたら練習にならないじゃん。
それでは今度は \((4,4)\) でやってみるよ。
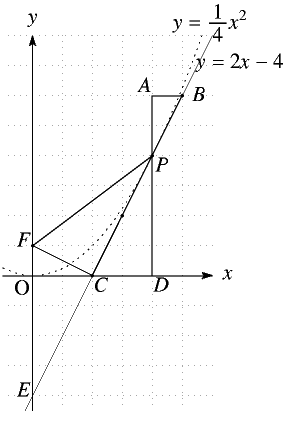
接線は \(y=2x-4\)
それにさっきは合同を使って考えたのが失敗だったとわかった。
それだけでも進歩だって。
今度は相似を使って考えてみようと思う。
角が等しければいいんだから相似で十分だよ。
まず\(\triangle PAB\)と\(\triangle PDC\)が相似なのは明らか。
対頂角は等しいし、いずれも直角三角形だからね。
この\(PC\)の傾きが2だから\(C\)で直角に曲がって、\(PC:CF=2:1\) になるように点を取ると
\(F(0,1)\)に来た!
銀さん 本当に\(\angle APB\)と\(\angle FPC\)は等しいと確認した?
金さん 2組の辺の比とその間の角が90度で等しいから\(\triangle APB\)と\(\triangle CPF\)は相似。
したがって相似な図形の対応する角は等しいから
\(\angle APB=\angle FPC\)
完璧だね。
銀さん \(P\)がどこでも同じようにできそうね。
金さん もうちょっと具体例で調べてみようか。
\(P(6,9)\)の場合は接線は \(y=3x-9\)
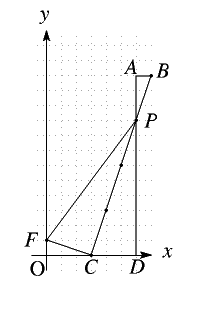
\(C\)の座標は\((3,0)\)だから
ここから傾き \(-\displaystyle\frac13\) で曲がると\(\ldots\) \(F(0,1)\)だ。
そうか\(C\)は必ず\(OD\)の中点に来るみたいだね。
\(P(8,16)\) の場合は接線は \(y=4x-16\) で \(C(4,0)\)
ちゃんと\(F(0,1)\)を通るね。
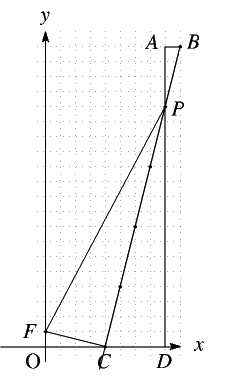
銀さん 私が \(P\left(p,\displaystyle\frac14p^2\right)\) でやってみるわ。
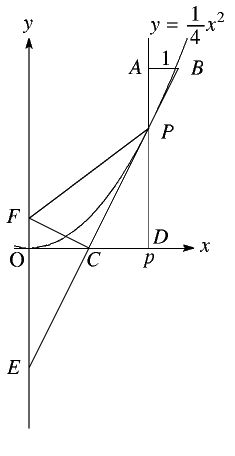
接線は \(y=\displaystyle\frac{p}{2}x-\displaystyle\frac{1}{4}p^2\)
\(AB=1\) となる \(\triangle PAB\) をとると \(AP=\displaystyle\frac{p}{2}\)
あれ、ということは \(\triangle COF\) と合同になる。
\(C\)が\(OP\)の中点になることをちゃんと証明しておこうか。
\(\triangle PDC\) と \(\triangle QOC\) が相似なのは明らか
\(PD=QO=\displaystyle\frac{1}{4}p^2\) だから合同がわかる
したがって \(DC=OC\)
金さん それじゃぁ完全に一般化した場合は僕が挑戦しよう。
いつも具体的な計算しかできないだろうと思われるのもしゃくだから。
まず \(y=ax^2\) 上の点 \(P(p,ap^2)\) で直線 \(x=p\) が反射するとする。
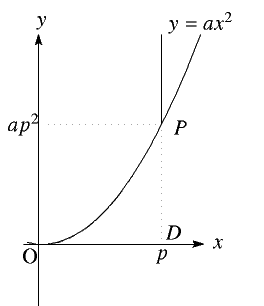
図のように \(AB=1\) となるように \(\triangle APB\) をつくる
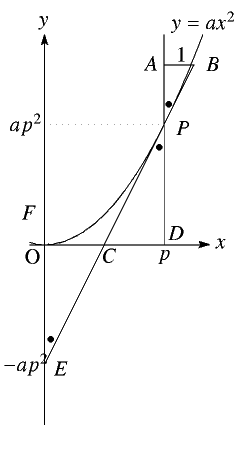
接線は \(y=2apx-ap^2\) なので
\(AP=2ap\) だ。
接線と\(x\)軸の交点を\(C\)とし、\(y\)軸上に\(PC\perp CF\) となるように\(F\)をとる。
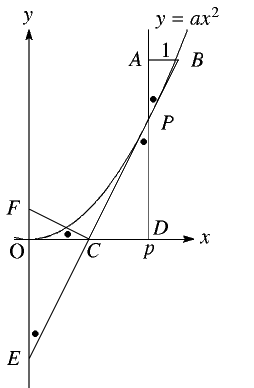
ここで
\(\triangle APB\sim \triangle DPC \equiv \triangle OEC \sim \triangle OCF\)
であることがわかる。
(日本では相似は「∽」だけど、\(\TeX\)では\(\sim\))
\(\begin{eqnarray*}
CD:DP &=& AB:AP \\
CD:ap^2 &=& 1:2ap \\
2apCD&=&ap^2 \\
CD &=& \displaystyle\frac{p}{2}
\end{eqnarray*}\)
と、\(C\)が中点であることを計算でも確認できた。
したがって
\(OC=p-\displaystyle\frac{p}{2}=\displaystyle\frac{p}{2}\)
これを用いて\(F\)の座標を求める。
\(\begin{eqnarray*}
OF:OC &=& 1:2ap \\
OF:\displaystyle\frac{p}{2}&=&1:2ap \\
2apOF &=& \displaystyle\frac{p}{2}\\
OF &=& \displaystyle\frac{p}{2\times2ap}\\
&=&\displaystyle\frac{1}{4a}
\end{eqnarray*}\)
最後に\(PF\)を結ぶ。
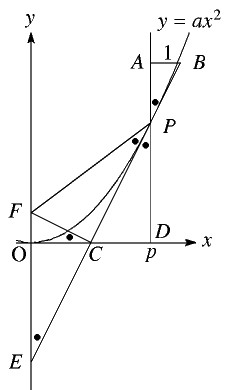
\(\begin{eqnarray*}
FC:CP &=& OF:CD \\
&=&\displaystyle\frac{1}{4a}:\displaystyle\frac{p}{2}\\
&=&1:2ap\\
よって\triangle CPF &\sim&\triangle APB\\
∴ \angle APB &=& \angle CPF
\end{eqnarray*}\)
よって\(P(p,ap^2)\) における反射は \(F\left(0,\displaystyle\frac{1}{4a}\right)\) を通る。
これでできたでしょ!
玉さん よくできました。
この点\(F\left(0,\displaystyle\frac{1}{4a}\right)\) を\(y=ax^2\) の焦点と言います。
でもまだ100点ではないわね。
金さん え~!まだダメなの!?
玉さん もう一息なんですが。それは宿題にしましょう。
宿題
上の続きを考えて、抛物線を用いてアンテナが作れることを示しなさい。
Tweet