図の直線ABの式を求めなさい。
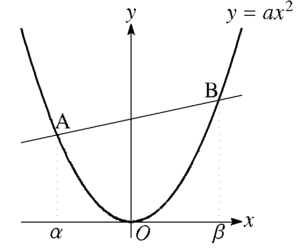
金さん なにこれ。文字しかないじゃん。
こんなのどこから手をつけたらいいのかわからないよ。
銀さん いつも言われているじゃない。
難しい問題に当ったら、易しい問題で練習をする。
金さん そうか。それじゃ、全部数字を入れてやってみよう。
\(a=1\), \(\alpha=-2\), \(\beta=3\) にしようかな。
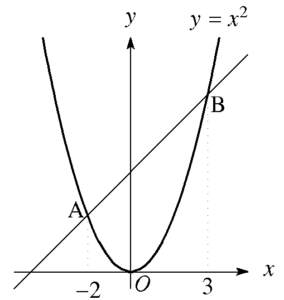
金さん これなら教科書レベルだからできそうだ。
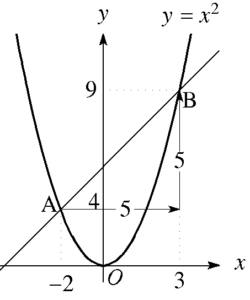
まず、AとBの座標を求めよう。
\((-2)^2=4, 3^2=9\) だからA(\(-2,4)\), B\((3, 9)\)だ。
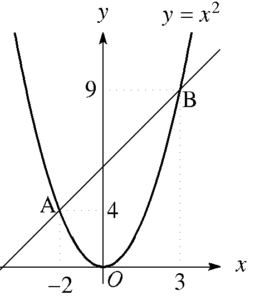
金さん これで直線ABの式を\(y=ax+b\)とおいて\(a\)と\(b\)についての連立方程式を解けば良い。
\(\begin{cases}-2a+b=4 \\ \hspace{2.2mm}3a+b=9\end{cases}\)
これを解いて
\(\begin{cases}a=1 \\ b=6\end{cases}\)
したがってABの式は
\(y=x+6\)
できたぁ。
銀さん 連立方程式を使うのも良いけれど、傾きと切片を考えた方が早いのではないかしら。
ABの傾きは
\(xの増加量=3-(-2)=5\)
\(yの増加量=9-4=5\)
したがって
\(傾き=\displaystyle\frac{5}{5}=1\)
銀さん
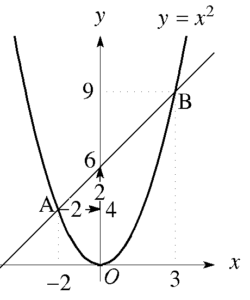
ということは切片はAから右に2増加しているのだから
\(4+2=6\)
つまり傾き1、切片6の直線だから
\(y=x+6\)
金さん なるほどね!
それじゃ。最初の問題についてその方法でやってみるよ。
A\((\alpha,a\alpha^2)\), B\((\beta,a\beta^2)\)を
\(y=px+q\)に代入して、
\(連立方程式\begin{cases}\alpha p+q=a\alpha^2 \\ \beta p+q=a\beta^2\end{cases}\)
を解くのは気が進まなかったんだ。

金さん まずABの傾きを求めよう。
\(xの増加量=\beta-\alpha\)
\(yの増加量=a\beta^2-a\alpha^2\)だから
\(\begin{eqnarray*}
ABの傾き&=&\displaystyle\frac{a\beta^2-a\alpha^2}{\beta-\alpha}\\
&=&\displaystyle\frac{a(\beta^2-\alpha^2)}{\beta-\alpha}\\
&=&\displaystyle\frac{a(\beta+\alpha)(\beta-\alpha)}{\beta-\alpha}\\
&=&a(\beta+\alpha)
\end{eqnarray*}\)
おお、綺麗になった。
銀さん 切片は私がやりましょう。
今度は方程式を使った方がわかりやすいかしら。
切片を\(b\)とおいて、ABの式を
\(y=a(\alpha+\beta)x+b\)とする。
この式にA\((\alpha, a\alpha^2)\)を代入すると
\(\begin{eqnarray*}
a\alpha^2 &=& a(\alpha+\beta)\alpha+b\\
a\alpha^2 &=& a\alpha^2+a\alpha\beta+b\\
0 &=& a\alpha\beta+b\\
-a\alpha\beta &=& b\\
b&=&-a\alpha\beta
\end{eqnarray*}\)
切片は\(-a\alpha\beta\)とでたわ。
金さん これは綺麗な式だね。
\(x\)座標をたすと傾きがでて、掛けると切片がでるわけだ。
さっきの練習問題だと\(-2+3=1\)で傾きがでて、\(-(-2)\times3=6\)で切片がでる。本当だ!
これを知っていたら簡単だったのに。
玉さん そうですね。
公式として覚えておいて損はないでしょう。
2乗比例のグラフと交わる直線

\(\mbox{AB}の傾き=a(\alpha+\beta)\)
\(\mbox{AB}の切片=-a\alpha\beta\)
したがって
\(\mbox{AB} : y=a(\alpha+\beta)x-a\alpha\beta\)
金さん これは便利な公式だよね。
傾きは変化の割合と同じことだから変化の割合を求めるにも使える。
銀さん なぜ、この定理は教科書に載っていないのでしょうか。
玉さん それはね、先程傾きを求める中で\(\displaystyle\frac{\beta-\alpha}{\beta-\alpha}\)を約分しましたよね。
その部分が学習指導要領の定めている中学3年生の範囲から逸脱しているからです。
金さん そんな大人の事情なんですか。これ知っていると知らないとでは全然計算量が違ってくるのに。
玉さん それに\(\beta-\alpha\)でわるということは、微妙な問題もはらんでいるのです。
銀さん もしかしたら0になる可能性があるということですか?
金さん そうか。もし、\(\alpha=\beta\)だったら、\(\beta-\alpha=0\)になってしまう。
???ということはどうなるんだ?
玉さん 先程の議論はそういった粗雑な部分があり、そこで教科書は避けたといえるかもしれません。
そこを丁寧に突っ込んでいったら、それこそ高校レベルになってしまいますから。
銀さん でも、とても便利な公式ですから\(\alpha\ne\beta\)の条件をつけて、教科書に入れておいて欲しいと思いますね。
玉さん ふふふ。実は面白いことに、この公式は\(\alpha=\beta\)でも成立するのです。
金さん えっ!?
\(\alpha=\beta\)ということはAとBが一致するということ。
どんな図になるんだろう。
銀さん 接線ですね。
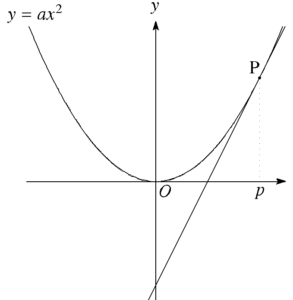
玉さん そのとおりです。
\(\alpha\ne\beta\)の条件は忘れて、機械的に\(\alpha\)と\(\beta\)に\(p\)を代入してみてください。
金さん それくらいなら僕がやろう。
傾きは
\(\begin{eqnarray*}
a(\alpha+\beta)&=&a(p+p)\\
&=&2ap
\end{eqnarray*}\)
切片は
\(\begin{eqnarray*}
-a\alpha\beta&=&-app\\
&=&-ap^2
\end{eqnarray*}\)
ということはPにおける接線の式は
\(y=2apx-ap^2\)
玉さん そういうことです。
Pの\(y\)座標が\(ap^2\)ですから、切片の\(-ap^2\)はちょうど正負が逆ですね。
下の図で\(\mbox{PQ}=\mbox{QR}\)となるわけです。
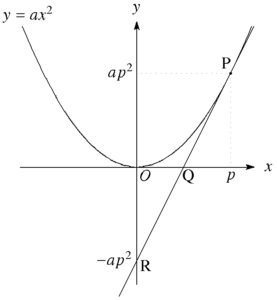
玉さん これを定理にしておくと、抛物線の重要な性質について話ができるのですが、今日はもう時間切れです。この話はまたの機会に続きを書きます。
2乗比例のグラフの接線

\(\mbox{PR}の傾き=2ap\)
\(\mbox{PR}の切片=-ap^2\)
したがって
\(\mbox{PR} : y=2apx-ap^2\)
宿題
- \(x\)軸を幅\(h\)で均等に分割する。それぞれの\(x\)座標に対応する\(y=ax^2\)上の点を、最初の2点は任意に選び結ぶ。
以降は順にその1つ外側同士、または内側同士を順に結んでいく。これらの線分がすべて平行になることを証明せよ。
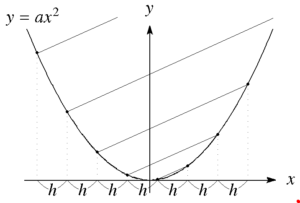
- すべての抛物線(\(y=ax^2\))は相似であることを証明せよ。