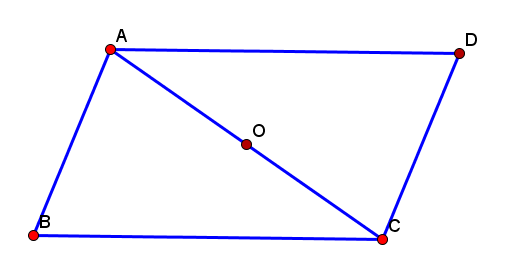
中学2年生の教科書には平行四辺形の性質が次のように記述されている。

平行四辺形の性質

1. 2組の対辺がそれぞれ等しい。
2. 2組の対角がそれぞれ等しい。
3. 対角線がそれぞれの中点で交わる。

つまりは平行四辺形は点対称だということだ。

点対称とは180度回転しても合同な図形だと言うことだから、上の性質では3番が本質だといえる。

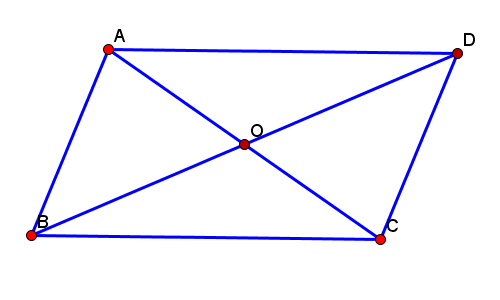
すなわち\(OA=OC, OB=OD\)を示すことで、対角線の交点Oが回転の中心であり、AがCに、BがDに180度の回転移動で移ることが示される。

ところが3番をいきなり証明しよう、すなわち\(\triangle OAB\equiv\triangle OCD\)を示そうとしてもうまくいかない。
平行四辺形という仮定(2組の対辺がそれぞれ平行)だけでは、どこも辺が等しいことがいえないからだ。

そこで1番を先に証明することが必要になる。

まとめると平行四辺形の性質は

• 3が本質。
• 1は3を証明するための補題。
• 2は1の証明から獲れるオマケ。

このように理解していた。

しかし、よく考えてみると、1番の証明をすればもう充分という気がしてきた。

1番の証明をするためには角辺角の合同条件を用いて\(\triangle ABC\equiv\triangle CDA\)を示す。

これで直感的には平行四辺形が点対称だと主張しても良さそうだ。
点対称であることを証明するには平行四辺形ABCDと平行四辺形CDABが合同であることを示せば良い。
それは分解して\(\triangle ABC\equiv\triangle CDA\)と\(\triangle ACD\equiv\triangle CAB\)を示すことになるが、この2つは同じことだからだ。

合同な図形の対応する長さや角の大きさは等しいので、ACの中点をOとすると、中線の長さが等しいこともいえるから、\(OB=OD\)。さらに\( \angle AOB=\angle COD\)もいえるので、\(\angle BOD=180°\)もいえる。

Tweet