このテキストは関係ない話(43)抛物線の性質のつづきです。
2乗比例のグラフの接線
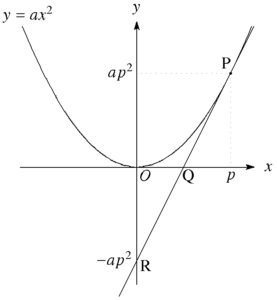
\(\mbox{PR}の傾き=2ap\)
\(\mbox{PR}の切片=-ap^2\)
したがって
\(\mbox{PR} : y=2apx-ap^2\)
この定理を承認して、抛物線の性質について調べます。
続きを読む 風みどりの詰将棋と関係ない話(45) 抛物線の性質(中学3年生向け)つづき
このテキストは関係ない話(43)抛物線の性質のつづきです。
2乗比例のグラフの接線

\(\mbox{PR}の傾き=2ap\)
\(\mbox{PR}の切片=-ap^2\)
したがって
\(\mbox{PR} : y=2apx-ap^2\)
この定理を承認して、抛物線の性質について調べます。
続きを読む 風みどりの詰将棋と関係ない話(45) 抛物線の性質(中学3年生向け)つづき
図の直線ABの式を求めなさい。
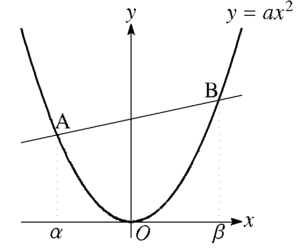
金さん なにこれ。文字しかないじゃん。
こんなのどこから手をつけたらいいのかわからないよ。
続きを読む 風みどりの詰将棋と関係ない話(43) 抛物線の性質(中学3年生向け)
はじめてのクラスで授業をするとき、「先生、自己紹介してください」という生徒がいる。
続きを読む 風みどりの詰将棋と関係ない話(40) 定番のマクラ
\(x^2+2x-15\)を因数分解しなさい。
ただし公式Iは使わないこと。
金さん これはやけに簡単。
かけて\(-15\),たして\(+2\)になるのは\(-3\)と\(+5\)だから
\((x-3)(x+5)\)
銀さん 問題をよく読まないと。公式Iは使っちゃ駄目と書いてあるよ。
金さん えっ、でもこれは公式を使って解く問題でしょ。
銀さん うーん。確かに。
続きを読む 風みどりの詰将棋と関係ない話(39) 因数分解の問題(中学3年生向け)
Tweet\(x^2=2\)という2次方程式を次のように解いてみる。
\(\begin{eqnarray*}
x^2 &=& 2 \\
x^2-1 &=& 2-1 \\
(x+1)(x-1) &=& 1 \\
xは1でも-1で&も&ないのは明らかなので\\
x-1 &=& \dfrac{1}{1+x} \\
x&=& 1+\dfrac{1}{1+x} \\
\end{eqnarray*}\)
続きを読む 風みどりの詰将棋と関係ない話(33) \(-\sqrt{2}\)は何処へ?
たまには数学の問題を考えて、頭をリラックスさせましょう。
もちろん私が出題するのですから、数学といっても義務教育レベルの問題です。
今日は美代子であることを証明してもらいます。
ここでいう美代子とは
のことではありません。
最小のピタゴラス三角形。3辺の長さの比が\(3:4:5\)である直角三角形のことです。
続きを読む 風みどりの詰将棋と関係ない話(21) こんな所に美代子が!
Tweet先日のプロパラ会で齋藤夏雄さんの『詰将棋の世界』出版裏話を楽しく聞かせていただいた。その中に、一松信先生からの1枚の葉書が連載第8回と9回を書かせたという話があった。
続きを読む 風みどりの詰将棋と関係ない話(6) プラトン多面体
詰将棋と関係のない話といっても「中学校」と「マンガ」の話を交互に書いているだけのような気がする。
オイラの人生ってそれだけだったのか?
で、順番からいって今日は「中学校」の話だな……。
続きを読む 風みどりの詰将棋と関係ない話(5) 累乗
根号(\(\sqrt{ }\))を導入する際に分数を持ち出すのはおそらく定跡だろう。
はじめて小学校で \(3\div7=\displaystyle\frac37\) という計算(?)を習ったときには、
「これって何も計算してないじゃん」
と思ったことだろう。
しかし \(\displaystyle\frac37\) という新しい数(有理数)も大小関係を比較できたり、和差積商が計算できたりしていくうちに、「これも一種の数の仲間なんだ」と認識するようになったはずだ。
2乗して2になる正の数を
\(1.4142135623730950488016887242097\cdots=\sqrt{2}\)
と表すのも同じことだ。
これから \(\sqrt{2}\) や \(\sqrt{3}\) といった根号の付いた数同志の大小関係を比較したり、和差積商の計算を考えていくうちに、「これも数の仲間に入れてやろう」という気になっていくと思いますよ。
もちろんお母さんに
「たかし~、3m の飴もらったんで家族7人で平等に分けたいんだけど1人分何cmに切ればいい?」
「ん~、\(\displaystyle\frac37\)m」
「たかし~、1辺1mの正方形の凧作りたいんだけど、対角線にする竹は何cmに切ればいい?」
「ん~、\(\sqrt{2}\)m」
いずれの答も「役に立たないね!」と叱られるのも一緒です。
続きを読む 風みどりの詰将棋と関係ない話(3) 余りのある割り算